Gequantiseerde hoeken

Eenheidhoek van de regelmatige zevenhoek
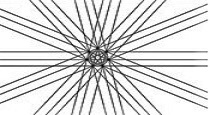
In een regelmatige zevenhoek worden alle diagonalen getekend.
Alle zijden en diagonalen worden in beide richtingen verlengd.
Dan ontstaat deze figuur met een wirwar van lijnen en hoeken:



In deze figuur komen alleen maar hoeken voor
die 1, 2, 3, 4 of 5 maal 180°/7 zijn.
Die 180°/7 noem ik de eenheidhoek van de regelmatige zevenhoek.
Ik noteer hem als u₇.

Alle mogelijke driehoeken in de regelmatige 7-hoek zijn van de vorm
(1,1,5)u₇, (1,2,4)u₇, (1,3,3)u₇ en (2,2,3)u₇.
Tussen haakjes staan de drie hoeken van de driehoek, uitgedrukt
in de eenheidshoek u₇. Diezelfde getallen staan ook in de tekening.
De som van de drie hoeken in een driehoek is steeds 180° = 7.
Daarom is in (bijvoorbeeld)(1,2,4)de som van de drie getallen steeds 7.
Immers is 180°/7 = u₇. Dus 7u₇ = 180°.
De volgene figuur, een deel vd vorige. Daarin
zie je in elke hoek het aantal u₇:



In de natuur en dagelijks leven zijn regelmatige 7-hoeken uiterst schaars.
Bekijk eens de munt van 20 cent: een regelmatige 7-hoek.
Op de rand staan 7 inkepingen ten gunste van blinden.

Eenheidshoek van de regelmatige n-hoek
Het mooie is, dat een gelijksoortige eigenschap
in elke regelmatige n-hoek bestaat.
n is een willekeurig telgetal groter dan 2.
Elke regelmatige n-hoek heeft zijn eigen eenheidhoek en is 180°/n.

Samenvatting
Als in een regelmatige n-hoek alle diagonalen getekend worden,
dan is elke hoek een veelvoud van 180°/n.
Ik was erg verbaasd, dat deze eigenschap nooit eerder was ontdekt in de afgelopen twee millennia!

Enige reeds bekende eigenschappen
De som van de hoeken van een regelmatige n-hoek is (n - 2)180°.
De hoeken van een (lege) regelmatige n-hoek zijn dan (n - 2)180°/n.

Het aantal diagonalen in een regelmatige n-hoek is n(n- 3)/2.

In de volgende tabel ziet u enige voorbeelden van
alle genoemde eigenschappen.

figuur	naam	aantal hoeken en zijden	aantal diagonalen	som van de hoeken	grootte van de hoeken in °	eenheid- hoek in °	verwant figuur
	gelijkzijde driehoek = regelmatige driehoek	3	0	180	60	60	delta
	vierkant = regelmatige vierhoek	4	2	360	90	45
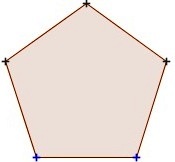
	regelmatige vijfhoek = pentagon	5	5	540	108	36	pentagram of 5-puntige ster alleen diagonalen
	regelmatige zeshoek	6	9	720	120	30	Davidster kerstster
	regelmatige 7-hoek	7	14	900	128 + 4/7	25 + 5/7	€ 0,20 munt
	regelmatige 12-hoek	12	54	1800	150	15	(analoge) klok
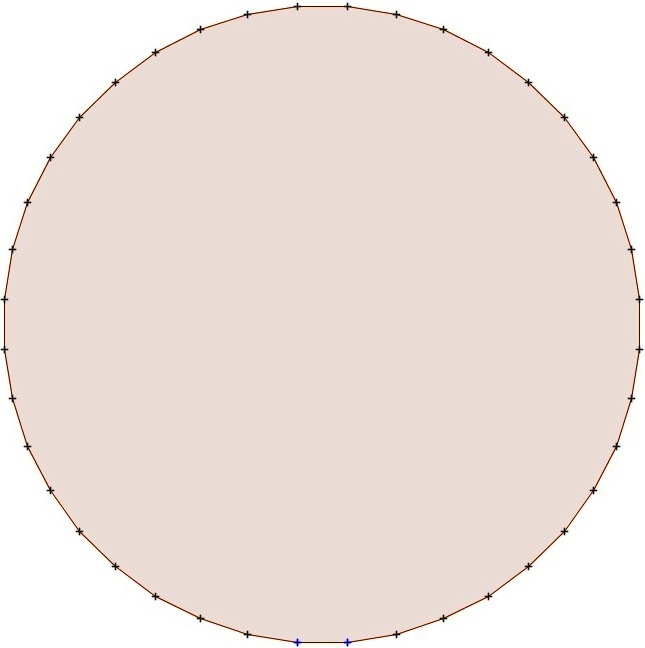
	regelmatige 360-hoek	360	64260	64440	179	1/2	bijna cirkel
	regelmatige n-hoek	n	n(n-3)/2	180(n-2)	180(n-2)/n	180/n

Het algemene bewijs is gebaseerd op de volgende meetkundige eigenschappen.

• 180° = n × u_n
• hoek + supplement = n × u_n
• overstaande hoeken zijn gelijk
• 2 × een omtrekshoek van een regelmatige
  veelhoek = middelpunsthoek.
• de omtrekshoek = de eenheidhoek
• de som van de hoeken in een driehoek is 180° = n × u_n
• de som van de hoeken in een vierhoek is 360°
• de som van de hoeken in een n-hoek is (n - 2) u_n
• spiegel- en rotatiesymmetrie van de figuur
• dat is alles, mensen!

spiegel- en rotatiesymmetrie

Wiskunde

Hoofdmenu